Сумма внутренних углов любого треугольника всегда равна 180 градусам. Это фундаментальное свойство евклидовой геометрии, справедливое для всех типов треугольников.
Содержание
Основная теорема о сумме углов треугольника
Доказательство теоремы
- Нарисуйте произвольный треугольник ABC
- Проведите через вершину B прямую, параллельную стороне AC
- Образовавшиеся углы при вершине B составят:
- Угол 1, равный углу A
- Угол 2, равный углу C
- Сумма углов 1, B и 2 составляет 180° (развернутый угол)
- Следовательно, ∠A + ∠B + ∠C = 180°
Примеры для разных типов треугольников
| Тип треугольника | Пример углов | Сумма |
| Равносторонний | 60° + 60° + 60° | 180° |
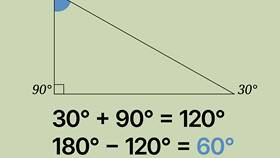
| Прямоугольный | 90° + 30° + 60° | 180° |
| Тупоугольный | 100° + 40° + 40° | 180° |
| Разносторонний | 70° + 60° + 50° | 180° |
Практическое применение свойства
- В строительстве при расчете конструкций
- В навигации для определения курса
- В геодезии при измерении участков
- В компьютерной графике при моделировании объектов
Интересные следствия
- Внешний угол треугольника равен сумме двух внутренних, не смежных с ним
- В прямоугольном треугольнике два острых угла в сумме дают 90°
- В равнобедренном треугольнике углы при основании равны
Теорема о сумме углов треугольника является одной из базовых в геометрии и находит широкое применение в различных областях науки и техники. Понимание этого свойства позволяет решать множество практических задач, связанных с измерением и построением треугольных конструкций.